An additional example to show posture multiplication between Concave & Convex tablocks. #26,Upright I Cave=312/332 as the multiplicand; #45,Averse E Cave=443/223 as the multiplier. Note the V/H paraperm arrangement for #28 Supine Y (Male mediate Q) below. The H component is reversed (4 becomes 2) from its Vertical component. Supine (V4) of a Male astral has a reversed horizontal (H2) of the vertical as 4/2 on the Female Concave tablock. Similarly, the V/H for #26 Upright E (Male immediate X) on the Concave has its Upright (1) reversed for the horizontal component of the paraperm 1/3.
To multiply #26 x #45, the troperm turns from the multiplier,#45 (HwD) are applied to the multiplicand,#26. Firstly, to do this, the "H" in the #45 troperm means a Horizontal reflection of #26 is made from Cave to Vex tablock. The reflex of #26 -Upright I Cave, is #2 -Upright I on the Vex tablock. The remaining turns (wD) are then done to #2 and the product is #12.
Since #26 has its principle perm as 213 and #45 has 312, when multiplying the two, the i,m,r principles in the multiplier must correspond to their same i,m,r principles above in the multiplicand. (#26)213=Jqx and (#45)312=xQJ. With the relfex applied from Cave to Vex, the Astral posture algorithm addresses this movement from interior(Cave) to exterior(Vex) of the tablock.
The Astral Posture algorithm establishes a reflex relationship between the Idemfactor #1(YIA) toperm and the Astral toperms for both the multiplicand(IUE) & multiplier(EYI) and their i,m and r posture paraperms. Then this arrangement is carried to the paraperm multiplication.
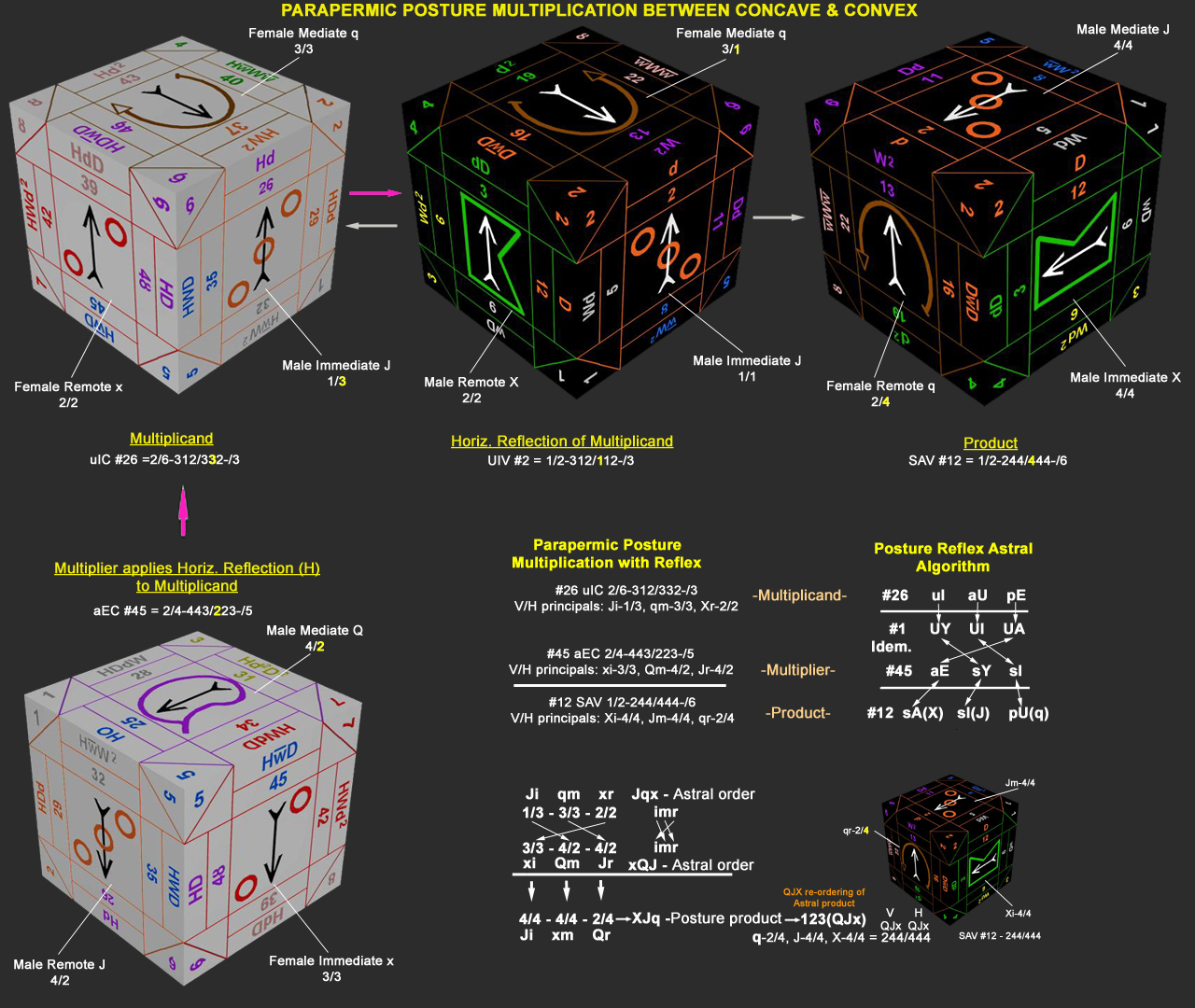
With a reflex from Cave to Vex, the relationship between multiplier & multiplicand is maintained through the Astral Posture algorithm with the idemfactor. We select the complementary principles between multiplier & idemfactor as follows: Upright Y of the idemfactor finds its principle supine Y in the mediate column. Bring down the multiplicand's principle Upright I above the idemfactor and place its product below the multiplier, which is supine I(J). Next, the Upright I of the idemfactor finds its principle in the remote multiplier of supine I. We bring down the averse U from the mutiplicand above, place its product below the multiplier as prone U(q). Lastly, the idemfactor of Upright A finds its principle in the multiplier as averse E. Bring down the multiplicand's principle of prone E and place the product beneath the remaining product place as supine A(X).
We then carry the multiplicand & multiplier i,m,r cross-arrangement from the Astral posture algorithm to the paraperm multiplication. The first perm 2 finds the i of #26 goes with the 1 perm m #45 and the product is put below in the 2 position (xm). Then the 1 perm of m #26 goes with the 3 perm of r #45 and the product is put below in the 3 place (Qr). Finally, the 3 perm of r #26 finds the 1 of i #45 and the product is put in the 1 position (Ji) below. For the three principal products we have: 2 perm=1/3x4/2(x)=4/4, 1 perm=3/3x4/2(Q)=2/4 & 3 perm=2/2x3/3(J)=4/4.
The V/H product postures are brought down as: 442/444 (JxQ). Since the principal order of the V/H parapermic operator (idemfactor) is always written in the Q,J,X sequence, the product's astral principals must be re-ordered in that manner.
So 442/444 (JxQ) is rearranged as 244/444 (QJx) for the final product: #12 SAV=1/2-244/444-/6.
CFR writes: "As the student grasps each concept & rule he, or she, should select & work many examples so as to fix them in the understanding & memory."
Next we will examine the perm order and how to determine its exact number.