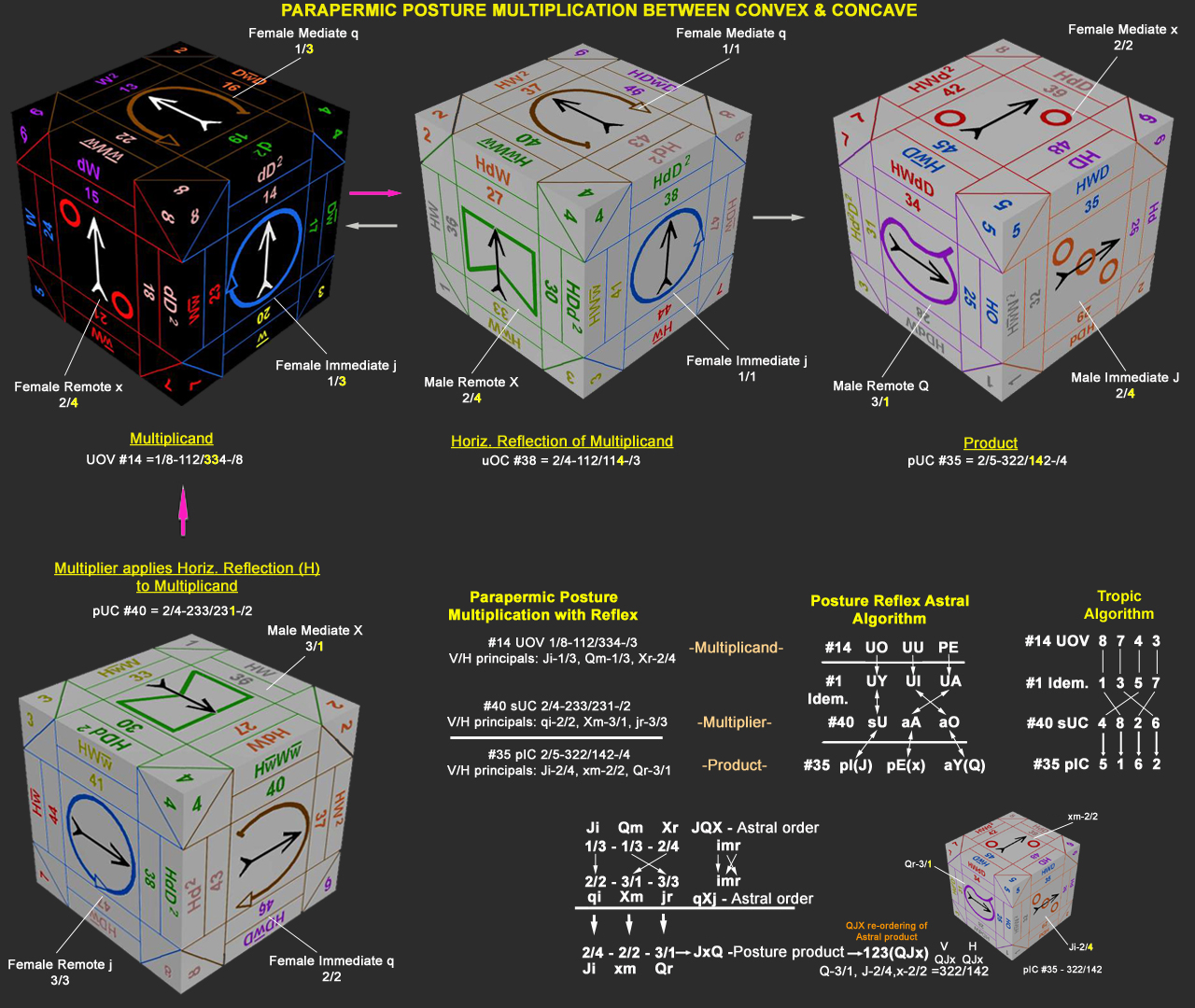
Here is an example of posture multiplication between Convex & Concave tablocks. #14,Upright O Vex=112/334 as the multiplicand; #40,Prone U Cave=233/231 as the multiplier. Note the V/H paraperm arrangement for #33 Averse A (Male mediate X) below. The H component is reversed (3 becomes 1) from its Vertical component. Averse (V3) of a Male astral has a reversed horizontal (H1) of the vertical as 3/1 on the Female Concave tablock. Similarly, the V/H for #36 Prone A (Male remote X) on the Concave has its Prone (2) reversed in the horizontal component of the paraperm 2/4.
To multiply #14 x #40, the troperm turns from the multiplier,#40 (HwWw) are applied to the multiplicand,#14. Firstly, to do this, the "H" in the #40 troperm means a Horizontal reflection of #14 must be made. We find the reflex of #14 -Upright O Vex, as #38 -Upright O on the Cave tablock. The remaining turns (wWw) are then made to #38 and the product is #35.
Since #14 has its principle perm as 213 and #40 has 231, when multiplying the two, the i,m,r principles in the multiplier must correspond to their same i,m,r principles above in the multiplicand. (#14)213=JQX and (#40)231=qXj. With the relfex applied from Vex to Cave, an additional Astral posture algorithm is required to address the reflex. Note that the i,m,r degree order of the multiplicand does not dictate the product ordering in the reflex case. The Astral Posture algorithm does this.
In much the same manner as the Tropic algorithm correlates the Idemfactor #1(1357) with the other I,M,N and R corners of the tablock faces, similarly, the Astral Posture algorithm establishes this same type of relationship between the Idemfactor #1(YIA) toperm and the other Astral toperms of both the multiplicand & multiplier i,m and r posture paraperms.
In the Astral Posture algorithm example above, the relationship between multiplier & multiplicand is established through the idemfactor. We select the complementary principles between multiplier & idemfactor as follows: Upright Y of the idemfactor finds its principle supine U in the same column. Bring down the multiplicand's principle Upright O above the idemfactor and place its product below the multiplier, which is prone I(J). Next, the Upright I of the idemfactor finds its principle in the multiplier of averse O. We bring down the Upright U from the mutiplicand above, place its product below the multiplier as averse Y(Q). Lastly, the idemfactor of Upright A finds its principle in the multiplier as averse A. Bring down the multiplicand's principle of Prone E and place the product beneath the remaining product place as prone E(x).
The product may also be verified, as shown above, using the tropic algorithm, e.g., #14(8743) x #40(4826) = #35(5162).
We then apply the multiplicand & multiplier arrangement from the Astral posture algorithm to the paraperm multiplication. Since the first perm 2 is identical between multiplicand & multiplier, the i of #14 goes with the i of #40 and the product is put below in the 2 position. Then the 1 perm of m #14 goes with the 1 perm of r #40 and the product is put below in the 3 place. Finally, the 3 perm of r #14 finds the 3 of m #40 and the product is put in the 1 position below. For the three principal products we have: 2 perm=1/3x2/2(J)=2/4, 1 perm=1/3x3/3(Q)=3/1 & 3 perm=2/4x3/1(x)=2/2.
The product postures are brought down as: 223/421 (JxQ). Since the principal order of the V/H parapermic operator is always written in the Q,J,X sequence, the product's astral principals must be re-ordered in that manner.
So 223/421 (JxQ) is rearranged as 322/142 (QJx) for the final product: #35 PIC=2/5-322/142-/4.
Let's continue working the parapermic multiplication from Concave to Convex tablock.