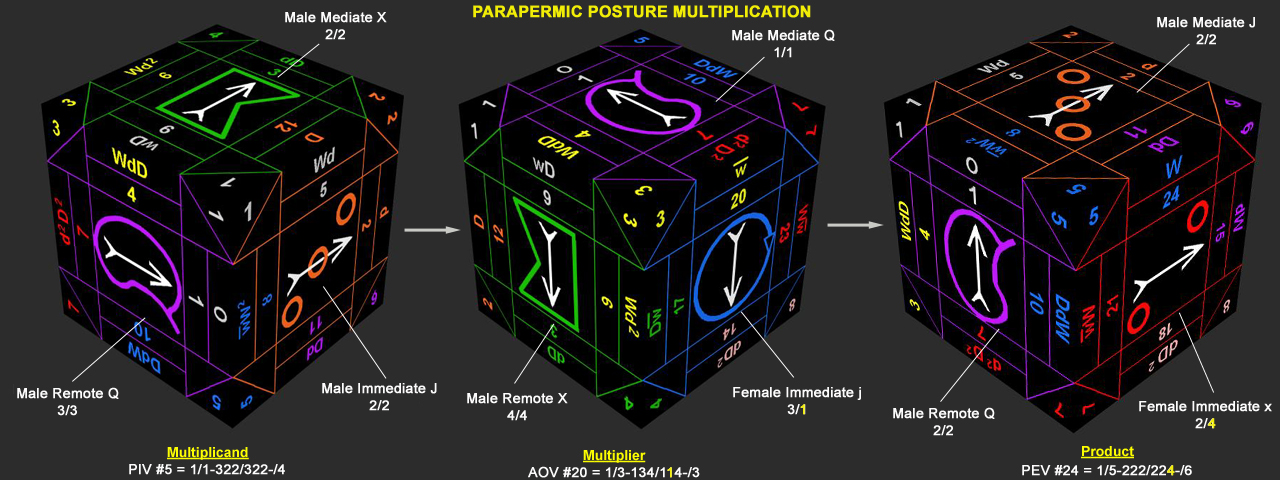
Letís take another example using #5,Prone I Vex=322/322 as the multiplicand; #20,Averse O Vex=134/114 as the multiplier. Note where female astrals (U, O or E) are present on the Male Convex tablock, the horizontal (H) portion of the paraperm is reversed. For example, see the V/H paraperm arrangement for #20 Averse O below. The H component is reversed (3 becomes 1) from its Vertical component. Averse (V3) of a Female astral has a reversed horizontal (H1) of the vertical as 3/1. This same rule applies, as we shall see later, for H components of male astral paraperms (Y, I and A) on the Female Concave tablock.
To multiply #5 x #20, the troperm turn from the multiplier,#20 (w) is applied to the multiplicand,#5. The product is #24.
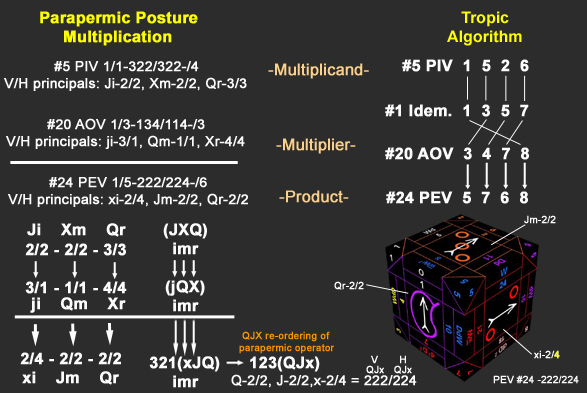
Since #5 has its principal perm as 231 and #20 has 213, when multiplying the two, the i,m,r principals in the multiplier must correspond to their same i,m,r principals above in the multiplicand. (#5)231=JXQ and (#20)213=jQX. The i of #5 goes with the
i of #20 and the product is put below in the i position since the principal order is governed by that of the *multiplicand* (#5). Then the m of #5 goes with the m of #20 and the product is put below in the m place (based upon the multiplicandís i,m,r). Finally, the r of #5 finds the r of #20 and the product is in the r position below. For the three principal products we have: i=2/2x3/1(x)=2/4, m=2/2x1/1(J)=2/2 & r=3/1x3/1(Q)=2/2.
The product postures are brought down as: 222/422 (xJQ). Since the principal order of the V/H parapermic operator is always written in the Q,J,X sequence, the product's astral principals must be re-ordered in that manner.
So 222/422 (xJQ) is rearranged as 222/224 (QJx) for the final product: #24 PEV=1/5-2 222/224-/6.
The product may also be verified, as shown below, using the tropic algorithm, e.g., #5(1526) x #20(3478) = #24(5768).
Next we continue by including the reflex (Vex/Cave) multiplication of the tablocks