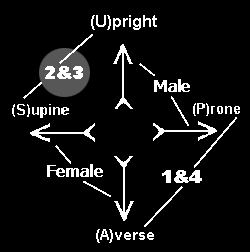
The four postures of each exact face are naturally divided into two classes of Horizontal & Vertical. Upright & Averse being the Vertical, while Prone & Supine are the Horizontal. Among each class there is a polarity of Male & Female. Upright & Prone being Male, while Averse & Supine are the Female polarity.
The Vertical or Horizontal posture for an adjacent face reached by a single turn is determined by the following general rules for the three principals (Q, X and J) of an exact face:
For Salt: A minor turn (d or w) from a Salt face (Q) always yields a vertical posture on the next face; a major turn (D or W) from Q gives a horizontal posture.
For Sulphur: A minor turn (d or w) from a Sulphur face (X) always finds a horizontal posture on the next face; a major turn (D or W) from X yields a vertical posture.
For Quicksilver: A minor or major turn from a Quicksilver face (J) in either case always produces a similar classed horizontal or vertical posture on the next face. That is to say, that if the J face has a vertical posture, then the next Q or X face reached by either minor or major turn will also have either an Upright or Averse posture. Likewise, if the J face is horizontal, it will be followed by either a Prone or Supine posture on the next face of the tablock. Verify these rules with both your Convex & Concave tablocks. Note: The above posture rules are somewhat related to the 'Egyptian' principle posture rules in Russell's Book BW.
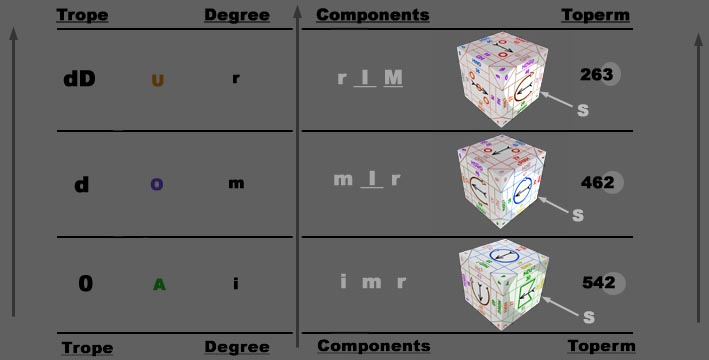
The first three components of a rational cradle are defined by the 0, d and dD turns from a designated exact face, which is the beginning (0) of a turn sequence. As in the previous examples of the Integral Closed Astralit, these three essential turns display the three principles of Q, J and X in six different posture perms or combinations. The three consecutive faces are named the Astral or (i)mmediate face, Vertical or (m)edite face, and Horizontal or (r)emote face. While moving through the three turns, if the principles of the faces change sex, they are capitalized in order to distinguish a change of their polarity. In other words, if the sex of a principle component changes through the three turns i would become I, m changes to M and r becomes R. Here is an example starting from our 0 face, Upright Y (Toperm 135):
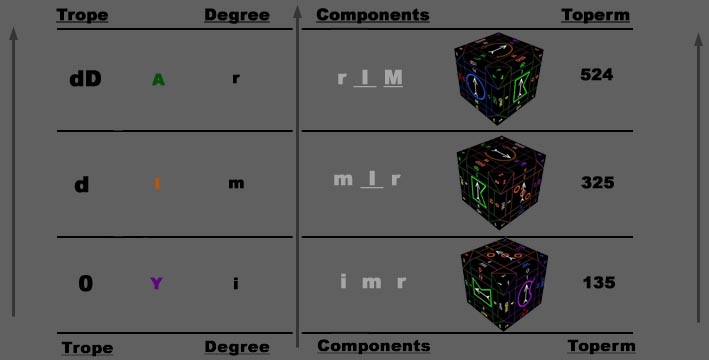
From the first position immediate degreeToperm, the subsequent mediate and remote degrees will easily be deduced. In the above example, note the change of sex first in the Q principle as it turns from Y to U in the second degree (m I r), and then continuing with the change in sex of the J principle in the third degree from I to O (r I M). In this case, the X principle remains as before and is not capitalized (r) since its polarity is not altered during the turns.
To continue, the Horizontal or Vertical parameter of a posture can be found by keeping in mind the above three rules of the principles for their minor and major turn relations. For example, with U-E-C (Upright E Cave 8765) the principle toperm is XQJ = 624. From X to Q is a minor d turn from X, hence the mediate face U has a Horizontal posture (P-U-C) with a Toperm of 254. In the next third degree turn, a major W turn from the Q results in a Horizontal posture for the remote J principle (S-I-C) with a Toperm of 352. See the table illustration below:
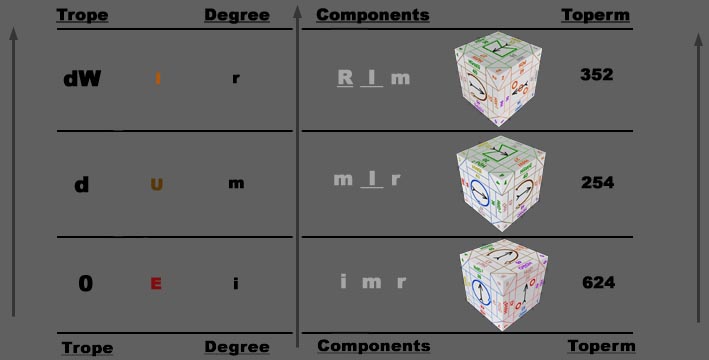
Further, we can deduce that the next face (mediate) from the J is always postured horizontally and its following remote face is postured vertically. In total there are only six different horizontal or vertical posture combinations for either the Vex or Cave tablock, which correspond to the six different principal perms.A table of the six posture perms and their corresponding principle perms to verify with your tablocks:
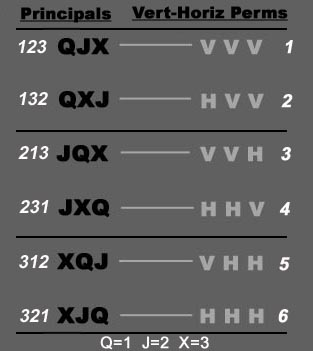
Conversely, we may also deduce from these Vertical-Horizontal Perms what the three corresponding Principals are which make up the immediate, mediate and remote faces of the Toperm. To continue, deriving the Male or Female portion of the posture is formulated by examining the i,m,r components of the Toperm. For example, take the Toperm 542; =XJQ as the i,m and r degrees where r(2) is less than m(4), hence the immediate face (A) is horizontal with the lesser r being 2, hence Supine. With the next mediate degree; 462=JXQ=m I r, whose r(2) is also less than the m(6), so the immediate face (O) of this degree is also horizontal with the lesser r again being 2 and thus Supine. Lastly, with the remote degree; 263=QXJ=r I M, the r(3) is again less than m(6) with the degreed face (U) as horizontal with the lesser r being 3, so again Supine.